How To Find Rate Of Change In An Equation
The Average Rate of Change part is defined as the average rate at which one quantity is irresolute with respect to something else changing. In simple terms, an average rate of modify function is a process that calculates the amount of modify in one item divided by the corresponding amount of change in another.
Formula for the Average Rate of Modify of a Function
Using function notation, we can ascertain the Average Rate of Change of a part f from a to b as:
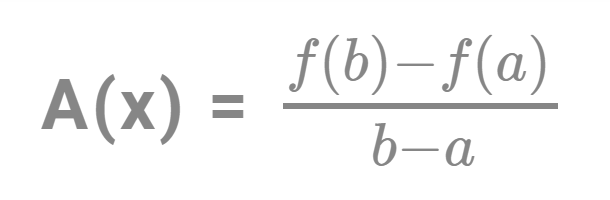
Where,
f(a) and f(b) are the values of the office f(x) at a and b respectively. Likewise, a and be are the limits of the function.
Solved Examples
Question 1: Calculate the average charge per unit of change of a function, f(10) = 3x + 12 equally x changes from 5 to viii .
Solution:
Given,
f(x) = 3x + 12
a = five
b = 8
f(v) = three(5) + 12
f(v) = 15 + 12
f(5) = 27
f(eight) = iii(8) + 12
f(8) = 24 + 12
f(8) = 36
The boilerplate rate of change is,
A(x) =
\(\begin{array}{l}\frac{f(b)-f(a)}{b-a}\end{assortment} \)
A(x) =
\(\brainstorm{assortment}{l}\frac{f(8)-f(five)}{8-5}\finish{array} \)
A(x) =
\(\begin{array}{50}\frac{36-27}{3}\end{assortment} \)
A(10) =
\(\begin{array}{l}\frac{9}{three}\cease{assortment} \)
A(10) = iii
Question two: Calculate the average rate of change of the function f(x) = x2 – 9x in the interval 2 ≤ x ≤ 7.
Solution:
From the given,
f(x) = 10ii – 9x
a = 2
b = 7
f(a) = f(two) = (ii)2 – 9(two) = 4 – 18 = -14
f(b) = f(seven) = (vii)2 – 9(vii) = 49 – 63 = -fourteen
The average charge per unit of change is:
\(\begin{array}{l}A(ten)=\frac{f(b)-f(a)}{b-a}\\=\frac{-14-(-fourteen)}{seven-2}\\=\frac{-xiv+fourteen}{5}\\=0\end{assortment} \)
Therefore, A(x) = 0
Source: https://byjus.com/average-rate-of-change-formula/
Posted by: jimenezressigirly1956.blogspot.com


0 Response to "How To Find Rate Of Change In An Equation"
Post a Comment